

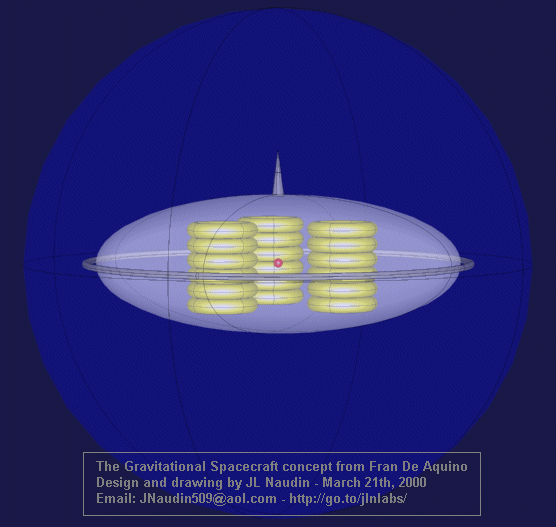
The
Gravitational Spacecraft from Fran De Aquino
Warping
to the deep space...
Courtesy of Fran De Aquino
created on March 21th, 2000 - JLN Labs - Last update April 20th, 2000
It is known that photons have null inertial mass (mi = 0 ) and that they do not absorb others photons (U = 0 ). So , if we put mi = 0 and U = 0 in Eq.(1.04),
![]()
the result is mg = 0. Therefore photons have null gravitational mass. Let us consider a point source of radiation with power P , frequency f and radiation density at distance r given by D = P /4p r2
Due to the null gravitational mass of the photons, it must be possible to build a shield of photons around the source, which will impede the exchange of gravitons between the particles inside the shield and the rest of the Universe. The shield begins at distance rs from the source where the radiation density is such that there will be a photon in opposition to each incident graviton . This critical situation occurs when D = hf 2 / Sg , where Sg is the geometric cross section of the graviton. Thus rs is given by the relation, rs = (rg / f )( P/h)1/2

We then see that the ELF radiation are the most appropriate to produce the shield. It can be easily shown that, if f << 1mHz , the radiation will traverse any particle . It is not difficult to see that in this case, there will be "clouds" of photons around the particles inside the shield. Due to the null gravitational mass of the photons , these "clouds" will impede the exchange of gravitons between the particle inside the "cloud" and the rest of the Universe. Thus, we can say that the gravitational mass of the particle will be null with respect to the Universe, and that the space-time inside the shield (out of the particles) becomes flat or euclidean . It is clear that the space-time which the particles occupies remains non-euclidean.
In an euclidean
space-time
the maximum speed of propagation of the interactions is infinite
![]() because , as we
know, the metrics becomes from Galilei.
because , as we
know, the metrics becomes from Galilei.
Therefore, the interactions are instantaneous . Thus , in this space-time the speed of photons must be infinite, simply because they are the quanta of the electromagnetic interaction. So, the speed of photons will be infinite inside the shield.
On the other hand , the new relativistic expression for mass, Eq.(2.06),
![]()
shows that
a particle with null gravitational mass isn’t submitted to
the increase of relativistic mass, because under
these circumstances its gravitational mass doesn't increase with
increasing velocity .i.e., it remains null independently of the
particle's velocity. In addition , the gravitational potential ![]() for the particle
will be null and, consequently , the component
for the particle
will be null and, consequently , the component ![]() of the metric tensor
will be equal to -1.
of the metric tensor
will be equal to -1.
Thus , we
will have ![]() where t' is the time in a
clock moving with the particle , and ds2
= c2
dt2
where
t is the time
indicated by a clock at rest ( dx = dy = dz = 0 ).
where t' is the time in a
clock moving with the particle , and ds2
= c2
dt2
where
t is the time
indicated by a clock at rest ( dx = dy = dz = 0 ).
From the
combination of these two equations we conclude that t' = t .This means that the
particle will be not more submitted to the relativistic effects
predicted in Einstein's theory. So, it can reach and even surpass
the speed of light . We can imagine a spacecraft with positive
gravitational
mass qual to (m) kg , and negative gravitational mass (
see System-G in appendix A) equal to - (m - 0.001) kg . It has a
shield of photons , as
above mentioned. If the photons, which produce the shield
,
radiate from the surface of the spacecraft ,
then the space-time that it occupies remains non-euclidean
,and
consequently , for an observer in this space-time , the total
gravitational
mass of the spacecraft, will be ![]() . Therefore , if its
propulsion system produces F=10N (only) the spacecraft acquires
acceleration
. Therefore , if its
propulsion system produces F=10N (only) the spacecraft acquires
acceleration ![]() ( see Eq.(2.05)).
( see Eq.(2.05)).
![]()
Furthermore, due to the "cloud" of photons around the spacecraft its gravitational interaction with the Universe will be null , and therefore, we can say that its gravitational mass will be null with respect to the Universe. Consequently, the inertial forces upon the spacecraft will also be null, in agreement with Eq.2.05 ( Mach’s principle ).This means that the spacecraft will lose its inertial properties . In addition, the spacecraft will can reach and even surpass the speed of light because , as we have seen , a particle with null gravitational mass will be not submitted to the relativistic effects.
Fran De Aquino, April 20th, 2000



See also :
The System-G Experimental setup tested by Fran De Aquino on January 27th, 2000
Engineering the System-G device by JL Naudin and Steve Burns
Reference documents :
The Gravitational Spacecraft by Fran De Aquino ( physics/9904018 )
Gravitation and Electromagnetism: Correlation and Grand Unification by Fran De Aquino ( gr-qc/9910036 )
![]() Email : JNaudin509@aol.com or mail to the JLN Lab's
eGroup at : jlnlabs@egroups.com if you are a team member.
Email : JNaudin509@aol.com or mail to the JLN Lab's
eGroup at : jlnlabs@egroups.com if you are a team member.
Return to the System-G home page