Propellant-less Electromagnetic Propulsion
By
Stavros G. Dimitriou
TEI-Athens, Dept. of Electronics Engineering
E-mail: dimsta@ee.teiath.gr
And
Dr. David King
The University of Manchester
Division of Electrical Engineering
E-mail: david.king@man.ac.uk
Abstract :
It is shown that the electric current and its rate of
change can emulate the physical velocity and acceleration
respectively. This emulation can be practically implemented, by
means of electronic circuits which demonstrate the physical
validity of the theory These electronic circuits are coupled to
specially shaped "antennas" which induce the relative
states of velocity and/or acceleration to the region of space
adjacent to them.
The relative state of velocity can be used to emulate the
condition of subjecting a mass to a centrifugal force relative to
the center of the Earth and lifting it. The relative state of
acceleration can be used to induce force and thus thrust on a
target mass.
The relevant circuits are compact, easily implemented and allow
the control of the intensity and the direction of the resulting
thrust force. Their "antenna" typically has the form of
a disk or rod, electrically behaving as a resonant tank circuit.
or plane capacitor, depending on case.
1. INTRODUCTION
We summarize below some concepts pertaining to propulsion and
their evolution into an ongoing, expanded research topic. This
work derives relationships linking the electric charge and its
time-derivatives with space and its time-derivatives too.
Implementation ideas are also presented, as well as techniques to
achieve control of the generated propulsion by electrical means.
2. DERIVATION OF THE BASIC RELATIONSHIPS
The derivation of the basic relationships can be found in
[1] The coupling formulae thus derived are the following,
assuming changes with time are sufficiently slow as to permit
considering for any practical purpose that the component of the
electric field is the dominant one:
![]() (1)
(1)
Taking the first and second derivative of eq.(1) with respect to time yields :
 (2)
(2)
and
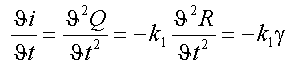 (3)
(3)
where ![]() and
and ![]() represent electric current,
velocity and acceleration, respectively.
represent electric current,
velocity and acceleration, respectively.
Equations (2) and (3) hint at the possibility of emulating
and/or substituting a physical velocity or acceleration by
an electric current and its derivative with respect to time.
The relevant vectors are coincident with the orientation of the
line extending from the source to the observer. while heir
direction depends on the sign of the corresponding derivative.
3. VELOCITY AND ACCELERATION FROM A PLANE
CAPACITOR
As reasoned in [1], similar equations can be derived for the case
of a plane capacitor:
 (5)
(5)
and
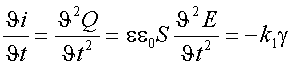 (6)
(6)
Where E and S stand for the intensity of the
electric field and the area of the plane capacitor, respectively.
Equations (5) and (6) suggest the possibility of generating a
field of velocity (simulating an inertial frame of reference) and/or
a field of acceleration by means of the electric field in a plane
capacitor [2]. Rod-shaped structures are also feasible..
4. HOVERING AT ALMOST NO ENERGY INPUT
The creation of a net lift force can be shown to be analogous to
developing a centrifugal lift on a body moving normal to the
terrestrial vector of gravity. A major advantage however is that
in using equivalent states of velocity, induced
electromagnetically, no physical movement of the body tangential
to the surface of the
Earth is needed. A further asset is that in inducing
electromagnetically the state of equivalent velocity, the actual
lifting energy is of relativistic origin and is supplied by
conversion of a tiny portion of the mass to be lifted into
equivalent potential energy. In this case, the electromagnetic
induction of the state or domain of equivalent acceleration
simply catalyses and sustains this energy conversion, as it
will be shown in the current Ph.D. work The result is a very high
efficiency in upward thrust generation. As no input energy is
demanded, the lifted body is isolated in its own frame of
reference and is therefore no subject to inertia.
It can be shown that the gain in height obtained by such a system is expressed by:
 (4)
(4)
where  , and I is
the current on the radiating structure R is the
mean Earth radius and go
is the gravitational acceleration on the surface of the Earth.
, and I is
the current on the radiating structure R is the
mean Earth radius and go
is the gravitational acceleration on the surface of the Earth.
The whole process is best attained in high-Q electromagnetic
resonators, such as specially shaped transmission lines and
cavities, with dimension from a fraction of the metre to several
metres across. The resonance frequencies involved range from VHF
down to HF respectively. It can be shown that the efficiency of
conversion grows with the volume of the relevant structure and
depends on the particular shape of the structure. Pan-cake or
convex-lens shaped cavities and transmission lines are strong
candidates in this application, aided by the utilization of
almost conventional RF power techniques [3].
5. WAVEFORMS USED
The electric waveforms used to generate the vectors of velocity
and/or acceleration must have dissimilar slopes between the
ascending and descending part of the signal. This is necessary in
order to obtain a non-zero sum of the derivatives per period.
Extensive analysis has been carried in [1] to optimize the
parameters pertaining to each particular waveform.
The efficiency of the electrically generating domains of velocity
and acceleration depends on the dimensions of the generating
element, with regard to the fundamental wavelength of the
waveform applied to it, as stated above.
6. MODULATED WAVEFORMS
In order to increase the efficiency of the radiating structure,
which is very low at relatively low frequencies, waveforms with
varying rise- and fall- slopes due to progressively varying
amplitude or frequency can be used.
The inherent advantage of the modulated waveforms is that almost
conventional techniques can be used to generate thrust from
appropriate radiating structures. A second advantage is that an
appropriately modulated RF carrier of a sufficiently high
frequency can be easily beamed and/or focused to a desirable
direction and object, in order to cause thrust generation on it.
The use of tuned parts of transmission lines and specially shaped
cavity resonators is implicitly imperative in terms of the Q
benefits it can provide. More advanced forms of modulation are
currently into investigation.
The sign of the acceleration can be controlled by the duty cycle
of the modulating waveform, which can also provide a neutral
position. Throttling action can thus be achieved, apart from the
possibility of controlling the amplitude through the power supply.
More advanced forms of carrier modulation are presently
researched on, providing a much higher yield.
7. IMPLICATIONS AND APPLICATIONS
The exploitation of the creation of states of equivalent
acceleration due to the second derivative of the electric charge
with respect to time can lead to the production of thrust vectors
of arbitrarily controlled orientation and amplitude. These
vectors can be used for space station keeping as a first
application, and as a substitute to more conventional thrusters
at a later stage of development. Thrusters in the form of RF-
resonant disks, rod-like transmission lines and plane-capacitor
banks are currently researched. Microwave stripline IC's for
thrust generation should also be possible to form.
8. ACKNOWLEDGEMENT
This work was initiated as an M.Sc./Ph.D. research at the
University of Manchester, supervised by Dr. David King [1].
Following its broadened interest [4] it is presently continued as
a joint research with the added cooperation of the Department of
Physics-Chemistry and Materials Technology (Prof.'s. N.Patarghias,
G. Kalkanis and D. Vattis) and the Department of Electronics
Engineering of TEI-Athens, in Greece.
References:
[1] S. G. Dimitriou, Radiation Phenomena of Specially Shaped
Current Pulses, M.Sc. Thesis, The University of Manchester, (1994).
[2] S. G. Dimitriou, Propulsive effect on a massive plane
capacitor driven by slope - asymmetric pulses, URSI International
Symposium On Electromagnetic Theory, 25-28 May 1998, pp. 805-7,Thessaloniki,
Greece.
[3] S. G. Dimitriou, On the pendulum oscillations of a suspended
RF resonant circuit, First antigravity conference, Reno, Nevada,
June 27-28, 1999.
[4] Thrust from time-derivatives of the electric charge, by S. G
.Dimitriou, a paper presented at the Greenglow project conference
at the University of Lancaster, on Sept. 3 1998, sponsored by
this University and British Aerospace.
This paper has been published on this web site, courtesy of Dimitriou Stavros
Return to the Field Effect Propulsion page