NOTHING IS SOMETHING: The Theory and Operation of a Phase-Conjugated Vacuum Triode Floyd A. "Sparky" Sweet - June 24th, 1988
THEORETICAL OVERVIEW
Nothing, on the cosmological scale, is virtually everything. It is the home of all the
invisible fields, rippling with the activity of every real force. Every kind of matter produces a
field, the field all mesh in complex ways, often causing interference with other fields. Fields
are the "stuff" of the virtual vacuum. A light particle is nothing more than a large interference
in the electromagnetic field. Apart from interaction with matter of other fields a field will not
be changed in the vacuum. It will not go away; it cannot. Fields are a fundamental part of the
vacuum structure itself. Fields in their most quiescent state form the virtual vacuum itself. Even
when everything that can be removed from a vacuum has been removed, the Higgs field remains.
``Imagine the entire universe permeated with a constant magnetic field''. One need not imagine,
for it is true. It is clear from experimentation that certain results appear that are not explainable
without the presence of a field. The field consists of an infinite number of one-dimensional
North and South poles in an incoherent state- incoherent due to the presence of a multitude of
other interfering fields formed by other North and South poles, or particles or quanta. Thus the
virtual vacuum is far from empty, far from nothing, it is rather seething with potential energy as
the primordial powerhouse of everything in the universe.
As postulated by Einstein in his famous equation E=MC^2 , energy is a kind of matter. So
even the energy of distant starlight must be accounted for in any holistic view of physical reality.
The vacuum itself is literally popping with virtual particles that appear and disappear in the field
during instants too brief to be measured. Virtual particles with lifetimes or dwelltimes too short
for the name "particles" to be appropriate. As a result the generated fields are always in some
state of flux. However, under the influence of a generated Motional Electromagnetic field parts
of the normally chaotic virtual field break off from randomness and form a more coherent region.
This region consists of a structured portion of the spacetime continuum which by its very nature
seems to attract more virtual particles (This increase in particle density has been verified by lab
experiments conducted the week of June 19, 1988). This higher concentration of particles develops
a warping of the spacetime continuum where negative energy is produced in abundance. The
existence of this condition via direct engineering of the virtual state allows for the safe generation
of electrical energy. This condition, in essence, forms the underlying principle of operation of
the Phase-Conjugated Vacuum Triode. This device, however, produces negative energy which
is the reverse of the conventional positive energy generated by all devices in service today. The
arc generated by a short-circuit in a negative energy system is excessively bright and cold,
producing barely an audible hiss with no explosive force. Melting of conductors does not occur
and this type of negative current passes through the human body with only the feeling of a chill.
Conductors remain cool under load while only tiny cross-sectional areas of copper are required
to convey many hundreds of watts of power. Although all of this seems nearly unbelievable,
only what has been demonstrated in the laboratory has been described in this paper. The source
of energy is unlimited, the virtual vacuum of space itself structured by a motional
electromagnetic field is the powerhouse.
THE NATURE OF SPACE
Space itself is the ability to accommodate energy. Consider for a moment the following
illustration:
A signal (energy) is transmitted from point A to point B. A and B are separated by a finite distance. Consider three periods of time:
- 1) The signal is launched from A.
- 2) The signal resides in the space between A and B.
- 3) The signal arrives at B.
If (3) occurs simultaneously with (1) we say that the signal has traveled at infinite velocity. The signal has never resided in the intervening space and therefore there exists no space between A and B. A is virtually at the same point in space as B. For real space to exist between A and B it is necessary that a signal travelling between them be "lost" with reference to both points for a finite period of time.
Now we know that for real space to exist between two points a signal travelling between
them will propagate at a finite velocity  . If a signal will not travel between two
points, as in the case when c=0, then we can also conclude that there is no link or intervening
space between them. We have no means of detecting either an infinite velocity-supporting space
or zero-velocity space, so they do not exist as usable scientific concepts. If space cannot
accommodate a signal it has no function and no reality. We are left then with the only real
space, the home of the real and virtual vacuum. Space which supports a finite, nonzero velocity
where
. If a signal will not travel between two
points, as in the case when c=0, then we can also conclude that there is no link or intervening
space between them. We have no means of detecting either an infinite velocity-supporting space
or zero-velocity space, so they do not exist as usable scientific concepts. If space cannot
accommodate a signal it has no function and no reality. We are left then with the only real
space, the home of the real and virtual vacuum. Space which supports a finite, nonzero velocity
where  .
The above discussion dealt with a definition of space and the propagation velocity it will
support. A similar argument applies to the impedance of space. A medium can only
accommodate positive energy if the medium resists it to a reasonable degree. Neither an
infinitely strong spring nor an infinitely weak one can absorb or accommodate energy by being
compressed. Neither an infinitely large mass nor an infinitely light mass can absorb or
accommodate energy imparted by collision. The same holds true for space. Energy cannot enter
space of zero impedance (i.e;
.
The above discussion dealt with a definition of space and the propagation velocity it will
support. A similar argument applies to the impedance of space. A medium can only
accommodate positive energy if the medium resists it to a reasonable degree. Neither an
infinitely strong spring nor an infinitely weak one can absorb or accommodate energy by being
compressed. Neither an infinitely large mass nor an infinitely light mass can absorb or
accommodate energy imparted by collision. The same holds true for space. Energy cannot enter
space of zero impedance (i.e;  ) any more than a force can bear on a mass of zero
magnitude. Similarly, energy could not enter space of infinite impedance. It follows therefore,
that necessary properties of real space are:
) any more than a force can bear on a mass of zero
magnitude. Similarly, energy could not enter space of infinite impedance. It follows therefore,
that necessary properties of real space are:
1) finite propagation velocity 2) finite impedance.
Continuing our discussion of space and the values of c, Zo, µ,we take as given that real space sustains non-zero finite impedance and velocity as follows:
 where: µ and
where: µ andare characteristics of a unit volume
As yet we have not arrived at volume, which implies real space. At this point in our discussion we have merely described c and Zo . Therefore, we can only define µ andin terms of them. Algebraically it can be shown that:
Although we have said that the fundamental characteristics of space are c and Zo , perhaps it is better to say that they are t and Zo , where t is the time delay through a finite segment of space replacing c, the velocity through that segment. It is profitable to move away from the idea of constant velocity c travelling through space which leads one to conceptualization of a segment of space which traversed in 1 nanosecond (nsec) is 1 foot long. If one starts with a conceptual frame in which space is in terms of t, a segment of space can easily be though of as 1 nsec wide, and the energy entering it appears leaving it 1 nsec later. Subsidiary concepts of length and velocity can then be deduced as needed. We could alternately say that space was (a) 1 foot wide with a propagation velocity of 1 foot/nsec, or (b) 2 feet wide with a velocity of 2 feet/nsec. Fundamental to the proposed world view is the reality that no experiment could help us decide between (a) and (b). The essence of space is time, not distance, and only one propagation velocity () is possible through a segment of space. Thus, time through a segment is intimately related to the length of the segment. Propagation which is not at the speed of light cannot exist according to this world view. GENERAL DESCRIPTION OF ENERGY TRANSFER Consider energy, flowing straight and level down the proximity of a transmission line. The energy does not know the width of the channel through which it is passing. If the energy reaches a point where the dielectric changes (but not the geometry), some of it will continue on and some of it will reflect. If the energy reaches a change in the width of the transmission line some will reflect and some will continue as well. The energy current will not know whether:
Energy current does not have directional inertia, so that (a) is equivalent to (b). Energy current does have an aspect ratio. If the aspect ratio is forced to change, some of the flowing energy will reflect in order to assure that its total aspect ratio remains constant. Crudely, the aspect ratio is similar to the ratio of E to H, or the same as the ratio ofto µ
. The aspect ratio of energy current is much like the aspect ratio of space. While the aspect ratio of space can change, it fundamental velocity
cannot really change. This parameter becomes merely our way of conceptualizing time delay when energy resides in a region of space.
A /B = Aspect Ratio
Uniform space has only two parameters:
- 1) aspect ratio
- 2) time delay
Aspect ratio defines the shape of energy entering a given region of space, but not its amplitude. Velocity or length define the time during which the properly shaped energy can be accommodated by a region of space. Aspect ratio is really a definition of the relative compatibility of adjacent regions of space. Does flowing energy current largely travel unimpeded through an interface, or does it largely reflect at the interface? Space has quiet zones through which energy glides virtually unreflected. There are also noisy zones where energy current becomes incoherent, bounces about and splits apart. Noisy zones in space have either rapidly changing geometry or rapidly changing impedance (). ELECTROMAGNETIC ENERGY The rate of flow of energy through a surface can be calculated as a function of E and H. Specifically this flow is equivalent to E.H per unit area. This energy flows at the speed of light through a medium where
. E and H are in quadrature and are normal to the direction of the energy flow. The energy density is therefore: E.H/c. If two signals of equal magnitude (assume E/2 & H/2) are travelling through each other in opposite directions the energy density is calculated as follows:
If the directions of the two signals are such that opposite H-fields cancel and E-fields add, an apparently steady E-field will be created. The energy density of the fields remain as calculated above, but the value of the E-field will double from E/2 to E. It is a simple matter using the equationsand
for a team wave to get rid of H and c and so convert the first equation into the well known equation for energy density in the so-called electrostatic field:
Similarly, if two signals flow through each other in such a way as to give the appearance of a steady magnetic field as a result of their E-field canceling it is easily shown using the above equations to cancel out H and c so that:
Modern physics is based upon the faulty assumption that electromagnetics contains two
kinds of energy: electric and magnetic. This assumption leads to a Baroque view of physical
reality. Under that view energy seems to be associated with the square of the field intensity
rather than a more reasonable view that it is linearly proportional to field intensity. It is worth
remembering that neither Einstein nor most modern physicists were or are familiar with the
concept of energy currents described herein. However, their work still survives by ignoring the
energy current concept, scalar electromagnetics, the works of T. E. Bearden, Kaluza-Klein, and
other who dispute Heaviside's interpretations of Maxwell's equations.
THE FALLACY OF DISPLACEMENT CURRENT
Conventional electromagnetic theory proposes that when an electric current flows down
a wire into a capacitor it spreads out across the plate, producing an electric charge on the plate
which in turn leads to an electric field between the capacitor plates. The valuable concept of
continuity is then retained by postulating ``after Maxwell'' a displacement current. This current
is a manipulation of the electric field (E) between the capacitor plates which has the dimensions
of electric current and completes the flow of electricity in the circuit. This approach permits us
to retain Kirchoff's laws and other valuable concepts even though superficially it appears that at
the capacitor there is a break in the continuous flow of electric current. The flaw in this model
appears when we notice that the current entered the capacitor at only one point on the capacitor
plate. We then are left with the major difficulty of explaining how the electric charge flowing
down the wire suddenly distributes itself uniformly across the entire capacitor plate, at a velocity
in excess of the speed of light. This paradoxical situation is created by a flaw in the basic
model. Work in high speed logic conducted by Ivor Catt has shown that the model of lumped
capacitance is faulty and displacement current is an artifact of the faulty model. Since any
capacitor behaves similarly to a transmission line it is no more necessary to postulate a
displacement current for the capacitor than it is necessary to do so for a transmission line. The
excision of ``displacement current'' from electromagnetic theory has been based on arguments
which are independent of the classic dispute over whether the electric current causes the
electromagnetic field, or vice versa.
THE MOTIONAL E-FIELD
Of all the known fields- electric, magnetic, gravitational and motional E-field- the only
ones incapable of being shielded are the induced motional E-field and the gravitational field. The
nature of the motionally induced electric field is quite unique; in order understand it more fully
we must start by parting with a few misleading paradigms. When magnetic flux is moved
perpendicularly across a conductor an electromotive force (e.m.f.) is electromagnetically induced
``within'' the conductor. ``Within'' is an artifact of the commonly used analogy comparing the
flow of electric current within a wire to the flow of water within a pipe. This is a most
misleading model theoretically. The true phenomenon taking place has little been thought of as
involving the production of a spatially distributed electric field. We can see that the model's
origins likely arose from the operation called ``flux cutting'', a most deceiving and misleading
term. A better term, ``time varying flux modulation'', does not imply any separation of lines of
flux. Truly, lines of flux are always in closure upon themselves and are mathematically
expressed as line integrals. It is fallacious to use the term ``cutting'', which implies time varying
separation which does not in fact ever occur. A motionally induced E-field is actually created
within the space occupied by the moving magnetic flux described above. This field is present
therein, whether or not a conductor is present in the space. In terms of a definition we can say
that, when magnetic flux of vector intensity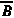 moved across a region of space with vector
velocity
moved across a region of space with vector
velocity , electromagnetically induced electric field vector BxV appears in the space at right
angles to both
, electromagnetically induced electric field vector BxV appears in the space at right
angles to both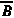 and
and  . Therefore,
. Therefore,
(1)
It is this field that is related to gravity, it is virtually unshieldable. This field may be called the
Motional E-field. According to T.E. Bearden ``It seems that the charged particles in the atom
(electrons and protons) act like tiny magnets. Their motion in the space surrounding the atom
would create this motional E-field''. The field created by both the positive and negative charges
would cancel to some degree, but due to the high orbital velocity of the negative electron relative
to that of the positive proton the induced field of the electron should dominate the resulting field.
The field produced as a result of these charges would vary proportionally to the inverse square
of distance similar to gravity. The field produced by the translational motion of the charges
would vary inversely as the cube of distance. This concept totally unites the electromagnetic and
gravitational field theories and accounts for the strong and weak forces within the atom.
FIELD SUPER-POSITION AND THE VACUUM TRIODE
Electromagnetic induction with no measurable magnetic field is not new. It is well known
that in the space surrounding a properly wound toroidal coil there is no magnetic field. This is
due to the superposition of the fields. However, when alternating current is surging through a
transformer an electric field surrounds it. When we apply the principle of superposition to the
vacuum triode it becomes more obvious how the device is in fact operating.
The principle of superposition states that ``In order to calculate the resultant intensity of
superimposed fields, each field must be dealt with individually as though the other were not
present''. The resultant is obtained by vector addition of each field considered singularly.
Consider for a moment the construction of the triode which includes the bifilar coils located
within the fields of the two conditioned magnets. When the current in one half of the conductors
in the coils (i.e., one of the bifilar elements in each coil) of the device is moving up, both the
current and the magnetic field follow the right-hand rule. The resultant motional E-field would
be vertical to both and inwardly directed. At the same time the current in the other half of the
conductors in the coils is moving down and both the current and magnetic field follow the right-
hand rule. The resulting motion E-field is again vertical to both and inwardly directed. Thus,
the resultant field intensity is double the intensity attributable to either one of the set of coil
conductors taken singularly. Expressed mathematically;
where:(2)
The first termin the equation represents the flow of the magnetic field when the electrons are moving in one direction, while the second term
defines the flow of the magnetic field when the electrons are moving in the other direction. These measurements indicate that field intensity is directly proportional to the square of the current required by the load placed on the device. This is due to its proportional relationship with the virtual value of the magnetic field which theory states is proportional to the current. Electrometer readings were always close to parabolic, thus indicating that the source was of infinite capacity. It was further determined through experiment that the magnetic field does not change with temperature. Also, there is no reason yet identified which would lead one to believe that electron drift velocity changes. It has been found remarkable that the vacuum triode runs approximately 20°F below ambient. INDUCED ELECTROMOTIVE FORCE - POSITIVE ENERGY When an e.m.f. is impressed on a closed metallic circuit, current results. The e.m.f. along a closed path C in space is defined as the work per unit charge (W/Q) done by the electromagnetic fields on a small test charge moved along path C. Since work is the line integral of force (F), the work per unit charge is the line integral of force per unit charge. Letting F/Q denote the vector electromagnetic force per unit charge (in newtons per coulomb) we have
(3)
The scalar product (F/Q) dtdl is the product of (F/Q) * cosdl with
denoting the angle between vectors F/Q and dl. The electric force per unit charge is the electric field intensity (E) in volts/meter. The magnetic force per unit charge is V x B where V denotes the velocity of the test charge in meters per second and B denotes the magnetic flux density in webers/M^2. In terms of the smaller angle
between V and B, the cross product of V and B is a vector having the magnitude VB sin
. The direction of vector VxB is normal to the plane which contains vectors V and B in accordance with the right-hand rule (i.e., VxB is in the direction of the thumb while the fingers curl through the angle
from V toward B). Since the total force per unit charge is E + VB the total e.m.f. in terms of the fields is:
(4)
It appears from eq. (4) that the e.m.f. depends on the forward velocity with which the test charge is moved along the path C. This, however, is not the case. If V and dl in eq. (4) have the same direction then their associated scalar product is zero. Thus, only the component of V which is not in-line with dl (i.e.=0) can contribute to the e.m.f.. This component has value only if the differential path length dl has a sideways motion. Thus, V in eq. (4) represents the sideways motion, if any, of dl. The fields E and B in eq.(4) could well be represented as functions of time as well as functions of the space coordinates. In addition, the velocity V of each differential path length dl may vary with time. However, eq. (4) correctly expresses the e.m.f. or voltage drop along path C as a function of time. That component of the e.m.f. consisting of the line integral V x B is the motional E-field since it has value ony when path C is moving through a magnetic field, traversing lines of magnetic flux. For stationary paths there is no motional E-field and the voltage drop is simply the integral of the electric field E. E.m.f.s are generated by devices that separate charge. A familiar example is the battery which utilizes chemical forces to separate charge. Other examples include the heating of a thermocouple, exposure of a photovoltaic cell to incident light, or the rubbing together of different materials (electrostatic charge separation). electric fields are also produced by time varying magnetic fields. This principle is extensively exploited to produce conventional electric power in the utility industry. The line integral of electric field intensity E around any closed path C equals -d
/dt, with
representing the magnetic flux over any surface S having the closed path C as its contour. The positive side of the surface S and the direction of the line integral around contour C are related by the right-hand rule (the curled fingers are oriented so as to point around the loop in the direction of the integration and the extended thumb points out the positive side of the surface S.) The magnetic flux
is the surface integral of magnetic flux density B as shown below:
(5)
In eq. (5) the vector differential surface ds has an area of ds and is directionally normal to the plane of ds out of the positive side. The partial time derivative ofis defined as:
(6)
This is referred to as the magnetic current through surface S. For moving surface S the limits of the surface integral in eq. (6) are functions of time but the equation is still applicable. It is important to clarify at this point that when we evaluate the value of d/dt over a surface that is moving in the proximity of magnetic field activity we treat the surface for the instant under consideration as though it were stationary. The partial time derivative of
is the time rate of change of flux through surface S due only to a changing magnetic field density B. Any increase of
due to the motion of the surface in the B-field is not included in that calculation. Continuing this discussion leads us to note that an electric field must be present in any region containing a time varying magnetic field. This is shown by eq. (7) displayed below:
(7)
In this equationis the magnetic flux in webers out of the positive side of any surface having path C as its contour. Combining e. (7) above with e. (4) we are able to calculate the e.m.f. about a closed path C. This is shown below:
(8)
and in another form
(9)
Thus, the e.m.f. around a closed path consists in general of two components. The component d/dt is the variational e.m.f. and the second component is the motional E-field. In eq.(9) (VxB)dl can be means of a vector identity be replaced with B*(Vxdl)A. V is the sideways velocity of dl, the vector Vxdl has magnitude Vdl and a direction normal to the surface ds swept out by moving length dl in time d. Letting Bn denote the component of B normal to this area we can see that -B*(vxdl) becomes -BnVdl and eq.(9) can be rewritten as:
(10)
Clearly, the integral of BnV around the closed contour C with sideways velocity of magnitude V for each length dl traversed is simply the time rate of change of the magnetic flux through the surface bounded by C. This change is due directly to the passage of path C through lines of magnetic flux. Hence, the complete expression of e.m.f. above in eq.(10) is the time rate of change of the magnetic flux over any surface S bounded by the closed path C, due to the changing magnetic field and the movement of the path through the magnetic field. eq.(10) may be written:
(11)
NOTE: The only difference between eq.(7) and eq.(11) is that eq.(7) contains only the variational e.m.f. while eq.(11) is the sum of the variational and motional emf's. In eq.(7) the partial time derivative of magnetic fluxis the rate of flux change due only to the time varying magnetic field while eq.(11) includes the total time derivative of the rate of flux change due to the time varying magnetic field and path C's passage through the magnetic field. If the closed path C is not passing through lines of magnetic flux then eq.(7) and eq.(11) are equivalent. It is also important to point out that d
/dt in eq.(11) does not necessarily mean the total time rate of change of the flux
over the surface S. For example, the flux over surface S is bounded by the closed contour C of the left portion of the electric circuit shown in Figure 1. The flux is
changing as the coil is unwound by the rotation of the cylinder as illustrated. However, since B is static there is no variational e.m.f. and since the conductors are not modulating lines of flux there is no motional e.m.f. Thus, d
/dt in eq.(11) is zero even the flux is changing with time. Note that d
/dt was defined as representing the right hand part of the expression in e.(10) and d
/dt must not be more broadly interpreted. In the application of the presented equations it is required that one refer all flux densities and movements to a single specified coordinate system. In particular, the velocities will all be with respect to this system alone and not interpreted as relative velocities between conductors or moving lines of flux. The coordinate system is arbitrarily selected and the magnitudes of variational and motional fields depend upon the selection. EXAMPLE #1 A fundamental electric generator is shown in Figure 2. The parallel stationary conductors separated by distance l have a moving conductor connected to across them.
The circuit is completed by a moving conductor connected to the parallel conductors by means of two sliding taps. This conductor is located at y=0 when time t=0, and moves to the right at a constant velocity V=Vay. The applied flux B is represented by dots on Figure 2 and has a magnitude that equals B=Bo cosBy cos wt ax. The unit vectors in the directions of the respective coordinate axes are ax, ay, and az. Solution: Let S denote the plane rectangular surface bounded by the closed electric circuit, with a positive side selected as the side facing the reader. The counterclockwise e.m.f. around the circuit is d
/dt with
signifying the magnetic flux out of the positive side of S (As ds=1 dy ax). The scalar product B*ds is Bo l cos By, cos
t dy; integrating from y=0 to y=y gives:
(12)
with y1 denoting the instantaneous y position of the moving wire. The counterclockwise e.m.f. is found by replacing y with vt and evaluating d/dt. The result is
(13)
The variational (transformer) component iswhich is determined with aid of eq.(12) to be
where y=vt. This is the first component on the right side of eq.(13). Note: y l was treated as a constant when evaluating the partial time derivative of
. The motional E-field is the line integral of V x B along the path of the moving conductor. As V x B is
and As dl is dz ax evaluation of the integral of
dz from Z=0 to Z=1 results in a motional E-field of
This component results from modulation of the lines of flux by the moving conductor. If the voltmeter draws no current, there can be no electromagnetic force on the free electrons of the wire. Therefore, the e.m.f. along the path of the metal conductors including the moving conductor is zero. EXAMPLE #2 Suppose the conductor with the sliding taps is stationary (V=0) and it is located at y=y 1 . Also suppose the magnetic field B is produced by a system of moving conductors not shown in Figure 2 which are travelling with a constant velocity V=Vay . At time t=0 the magnetic field B is Bo sinBy ax. Determine the voltage across the voltmeter. Solution: There is no motional E-field because the conductors in Figure 2 are at rest (stationary) with respect to our selected coordinate system. However, the magnetic field at points fixed with respect to the coordinate system is changing with time and as a result there is a variational e.m.f. Since the B-field at t=0 is B 0 sinBy ax and has a velocity of V=Vay it can be calculated that the B-field as a function of time is B o sin[B(y-vt)] ax. This is verified by noting that an observer located at y at time t=0 who is travelling at the constant velocity (V=Vay) of the moving current would have a y coordinate of y=y +Vt and an accordingly different expression for B. He would observe a constant field where the magnetic current density is:
The counterclockwise e.m.f. can be arrived at by taking the negative of an integral of the above expression for the rectangular surface bounded by the electric circuit with the positive side facing the reader with the limits of zero and y. The resulting e.m.f. equals:
which is the voltage across the meter. INDUCED MOTIONAL FIELD - NEGATIVE ENERGY Conventional theory says that electric fields and magnetic fields are different things. Consider for a moment a charge with an electric field around it. If the charge is moved a magnetic field develops and the moving charge constitutes a current. If an observer were to move along with the charge, he would see no relative motion, no current, and no magnetic field. A stationary observer would see motion, current and a magnetic field. It would appear that a magnetic field is an electric field observed from a motional reference frame. Similarly, if we take a mass with a gravity field around it and we move the mass and create a mass current, a new field is also created. It is a different kind of gravity field with no source and no sink. It is called the Protational field also known as the "Lense-Thirring Effect". This field an its governing principles will form the basis for future anti-gravity devices.Within the confined area of the Vacuum Triode box, the spacetime continuum is reversed by the fields that are produced in the presence of excited coherent space flux quanta. These quanta have been attracted from and ultimately extracted from the virtual vacuum, the infinitely non-exhaustible Dirac Sea. For a more detailed mathematical format see Appendix A, a paper on "The Phase Conjugate Vacuum Triode" by T.E. Bearden, April 23, 1987. Much of the theory which likely applies to the vacuum triode has been developed in the field of phase conjugate optics. With regards to over-unity phenomena it is important to note that so long as positive energy is present in a positive/flowing time regime unity and over-unity power gains are not possible. The summation of the losses due to resistance, impedance, friction, magnetic hysteresis and eddy currents and windage losses of rotating machinery will always reduce overall efficiency below unity for a closed system. The laws of conservation of energy always apply to all systems. However, the induced motional E-filed changes the system upon which those laws need be applied. Since the vacuum triode operates in dimensions more than four and provides a line between the multi-dimensional reality of the quantum state and a link between Dirac Sea we are now dealing with an open-ended system, not the closed system within which all conservation and thermodynamic laws were developed. To achieve unity, the summation of all magnetic and ohmic losses must equal zero. To achieve this state negative energy and resistance moves to zero and all energy flows along the outside of conductors in the form of a special space field. Negative energy is fully capable of lighting incandescent lights, running motors, and performing all of the functions of positive energy tested to date. When run in parallel with positive energy however, cancellation (annihilation) of opposing power types occurs. This has been fully tested in the laboratory. Once unity has been achieved and the gate to the Dirac Sea opened, over-unity is affected by loading the open gate more and more which opens it further to the point where direct communication/interaction with the nucleus of the atom itself is achieved. Output of the vacuum triode is not proportional to the excitation input as the output produced by the device is directly proportional to the load which is placed upon it. That load is the only dependent variable for device output. The triode's output voltage and frequency always remains constant due to the conditioning of the motional E-field in the permanent magnets and the small regulated excitation signal which is provided through a small oscillator. Regulation remains constant, output locks into an in-phase condition (cos
=1 Kvar=1) under all load characteristics. The vacuum triode is a solid state device consisting of conditioned permanent magnets capable of producing a motional field. This field opens the gate to the Dirac Sea where negative energy is able to flow from an into the triode's receiving coils. The coils are very small diameter copper wire but are capable of producing in excess of 5 kilowatts of useful power; this in itself is a clear indicator that the type of electrical energy provided by the device is not conventional. The wire sizes employed by the device would not be capable of carrying such large currents without excessive heat gain, however, the triode's coils actually run cooler when loaded at 5 kW. The fundamental magnets have been broken free of their binding forces which constrained them to be steadystate single pole uniform magnetic flux devices. They are now able to simply support mass, as demonstrated with the transformer steel illustration. They can now easily be made to adopt a dynamic motional field by applying a tiny amount of excitation. Specifically, 10V @ 1 mA (10 mW) of excitation at 60 Hz. will enable the coils of the triode to receive from the Dirac Sea in excess of 5000 watts of usable negative energy; how much more can safely be removed has not yet been determined.