This experiment is fully described in "The Feynman Lectures on Physics" :
Electromagnetism vol2, Chap: 26-2 by Addison-Wesley
Publishing company or collection InterEdition - ISBN
2-7296-0029-9.
A
- The
magnetic field created by a charged particle in motion
A charged particle in motion
produces a magnetic field that turns around the axis of
displacement.

B - The
Coulomb and Lorentz force between 2 charged particles in
motion
Let us consider the case of two
(positively) charged particles with charges Q1 and Q2
respectively, moving with speeds V1 and V2 on mutually
intersecting and perpendicular trajectories. The initial
position of Q1 is such that Q1 does not collide with Q2,
but instead arrives at the intersection point after
Q2.
Look at the animation above
carefully. Note that there is no magnetic field
along the trajectory of particle Q1 ( because particle Q2
has arrives at the intersection point before Q1 ).
Let us observe what occurs when particle Q1 arrives near
particle Q2 ( at the last stage of the animation ):
There is no magnetic
field along the axis of Q1, so Q2 is subjected
only to the electrostatic Coulomb force produced
by the electric field of Q1.
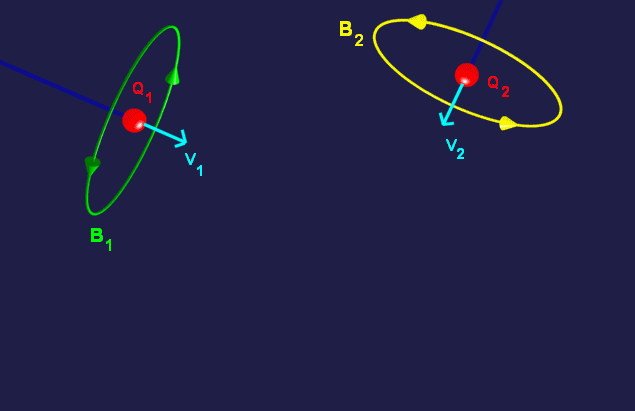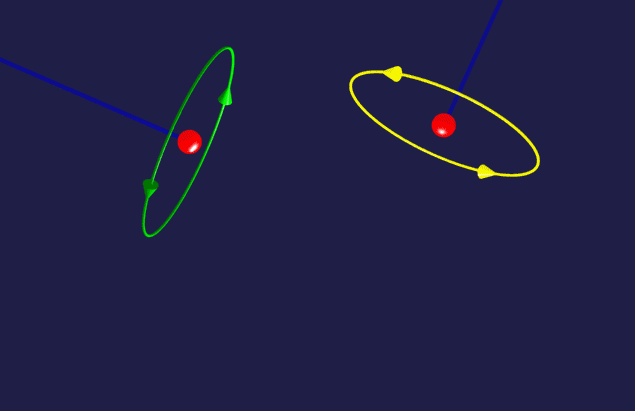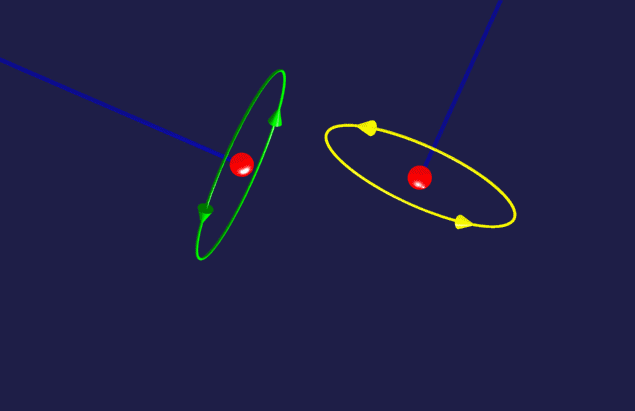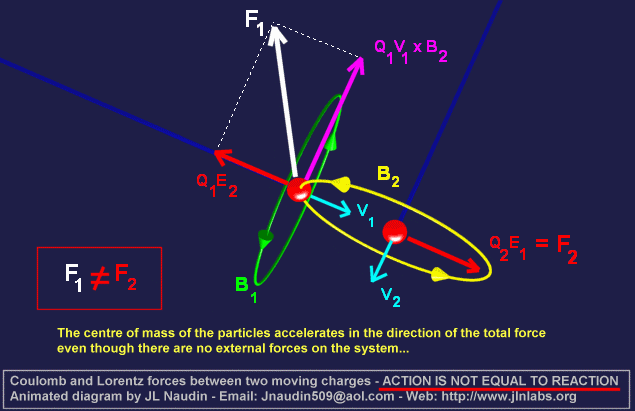
On the other hand, Q1 is
under the influence of the magnetic field
produced by Q2. In this case there are 2 forces
are involved : the electrostatic force produced
by the electric field of Q2 and the magnetic
Lorentz force produced by its own displacement
through the magnetic field of Q2.
The electrostatic Coulomb forces
are equal and opposite, so they validate
Newton's 3rd law, however there is a magnetic Lorentz
force on Q1 but no magnetic force on Q2.
Here we have a Force of ACTION WITHOUT a Force
of REACTION... In this case, Newton's
3rd law is invalidated.
The center of mass
of the particles Q1 and Q2 will accelerate
in a preferential direction without
any external force on the system...
Note
: To be in agreement with Newton's 3rd law, it would be
necessary to take into account the moments of the
magnetic and electric fields.
Reference
documents :
"The Feynman
Lectures on Physics" : Electromagnetism
vol2, Chap: 26-2 by Addison-Wesley Publishing
company or collection InterEdition - ISBN
2-7296-0029-9
La
Physique en MP - PC 1re Année - Volume 3 -
Electricité ( électromagnétisme ) par Pierre
Alais et Michel Hulin - Librairie Armand Colin.
 Very
interesting web site : Very
interesting web site :
Fundamentals of
Ether-based motion and Inner-ether
Energetics by G. P. Ivanov : http://www.tts.lt/~nara/intro.htm
|



