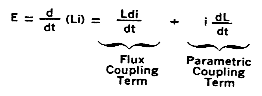
Equation #1
THE
PARAMETRIC POWER CONVERSION
A STEP TOWARDS
OVERUNITY......
Created on April 16th, 1997 - JLN Labs
- Last update : January 10th, 2003
Thanks to Fred B. Epps, Greg
Watson, Epitaxy
All informations in this
page are published free and are intended for private/educational
purposes and not for commercial applications
As shown by Equation #1, electromotive force, and hence the transfer of electrical energy can be achieved in two ways: (1) by flux coupling, or (2) by parametric coupling.
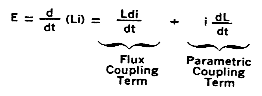
Equation #1
Consider a simple inductance (L) carrying a current (i) as shown in fig 1.
Fig 1
One knows that there is energy stored in this inductance of magnitude 1/2 LI*2 and if this inductance is now increased in some manner, such as by inserting an iron core into L (while holding I constant). then the stored electrical energy is increased. This is an example of parametric power transfer. (see Equation 1).
| Specials comments : "NO energy is required to insert the iron core into the inductor. It is ATTRACTED into the core and the resultant increased coil energy is pumped back into the power source (coil current drops)!" (Greg Watson) "No mechanical energy input is required to insert the iron core into the inductor, BECAUSE iron core is attracted by the inductor itself, thus no mechanical energy need to be expended !" (Epitaxy)
|
If in accordance whith Fig 2, the afore-mentionned core is now alternately inserted into and withdrawn from the inductance L and this inductance is, in turn a part of tank circuit, then a parametric oscillator result.
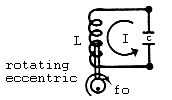
Fig 2
The most critical relationship associated with this parametric oscillator relate to frequency. For such devices, it is a well known fact that ideally, the pumping frequency (rotating eccentric) should be twice the frequency to which the resonant tank is tuned ( fig 3 ).
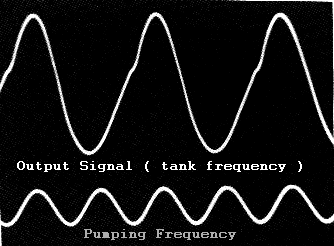
Fig 3
The following example demonstrate the general validity of this statement :
Assume that the current in the tank is oscillating at one-half the frequency of rotating eccentric ( see fig 4 ).
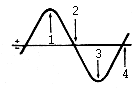
Fig 4
Current in LC Tank
Referring to fig 4, if the core is inserted at point (1) in the cycle, this increase in L, coupled with the large current flowing at that time, results in a large parametric energy transfer from the mechanism to the circuit. Furthermore, if the core is now withdrawn one-half of a mechanical cycle later (or one-quarter of an electrical cycle at point (2), the current is now zero and no electrical energy is withdraw from the tank. Similarly at point (3) we have additional parametric energy transfer and at (4) no transfer. Thus, by doubling the pumping frequency, power can be unilaterally transferred parametrically in accordance with the second term of Equation 1.

Fig 5
Parametric amplification of energy
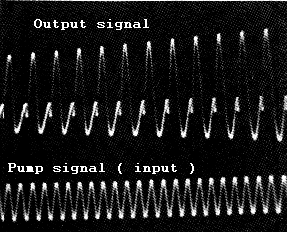
Fig 6
Transient state ( start of parametric amplification
)
In the example cited above, a mechanical driver was used. The final step, of course, is to achieve a simple passive all-electrical parametric device in which the double frequency pumping action is an intrinsic part of the device.
( Ref document : The PARAFORMER (TM), "A new passive power conversion device" by Dr S.D.Wanlass and Dr L.K. Wanlass )
Return to Parametric Home page or Return to Home page