
The Howard Johnson's permanent magnetic motor
created on 03/04/98 - JLN Labs - last update on 01-02-01
The Johnson's permanent magnetic motor uses the principle of a constant imbalance of the magnetic forces between the rotor and the stator. This permanent imbalance of the forces must be always maintained in the same direction during the complete revolution of the rotor (0 to 360 degres). By this way, the only source of energy will be the magnetic energy from the magnets.
I have made a closed loop simulation
with the QuickField software, but it is not necessary in this
case because, as you can see in the QuickField picture below, the
magnetic configuration is periodic. The magnetic configuration is
reproduced every 45 degres.
I have noticed in my design that the shape of the little curved
magnet (the magnet actuator) is very important and also the gap
between the rotor and the stator. In most cases of configuration
(shape and gap), the rotation stops, because the magnet actuator
blocks on a reversed magnetic field density. I have checked this
with the QuickField simulator, and this causes to me some
difficulties to find the correct setup. Today, I think that I
have understood how to tune the Johnson's motor.
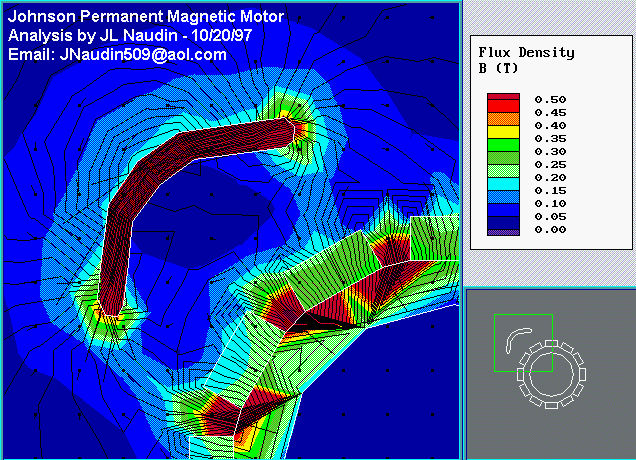
In this picture below, you see the global setup of this permanent
magnetic motor.
You will find below an example of the
magnetic flux density around the actuator magnet ( the small
boomerang). This is the most important thing to understand.
In the magnetic flux density curve you will see two troughs in
the curve, the first is the flux density above and the second is
flux density under the actuator. You will notice three peaks :
the first and the last are the south pole of the magnet and the
middle peak is the north pole.
The MOST IMPORTANT THING for obtaining a continuous rotation of
the PMM is that the flux density of the north pole MUST BE ALWAYS
LOWER than the flux density of the south pole. If this condition
is always obtained, for EVERY ANGLE of rotation, the PMM can turn
continuously. :-)
If unfortunately, for only one angle, the
flux density slope reverses, then the PMM will stop..... :-(
Today I have found the correct setup for obtaining this condition
for all the angles....

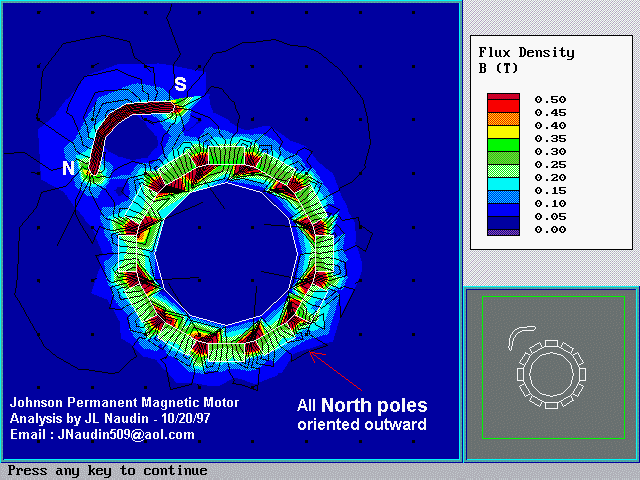
You see below, the first decisive document about the Johnson PMM, as you can see in the main picture of the motor, the magnet actuator rotates around the magnets ( the reciprocal is possible ). The geometric configuration is repeated every 45 degres, thus this is the period. In my simulation I have included 12 magnets with a step angle of 30 degres. Also the simulation includes the COMPLETE SETUP of the final design because the main problem of all PMM is the closed loop, this is the reason why I have used the complete configutation. You notice that the zero field edge is placed far around the PMM and it is CIRCLE SHAPED for avoiding all interferences with the PMM simulation.
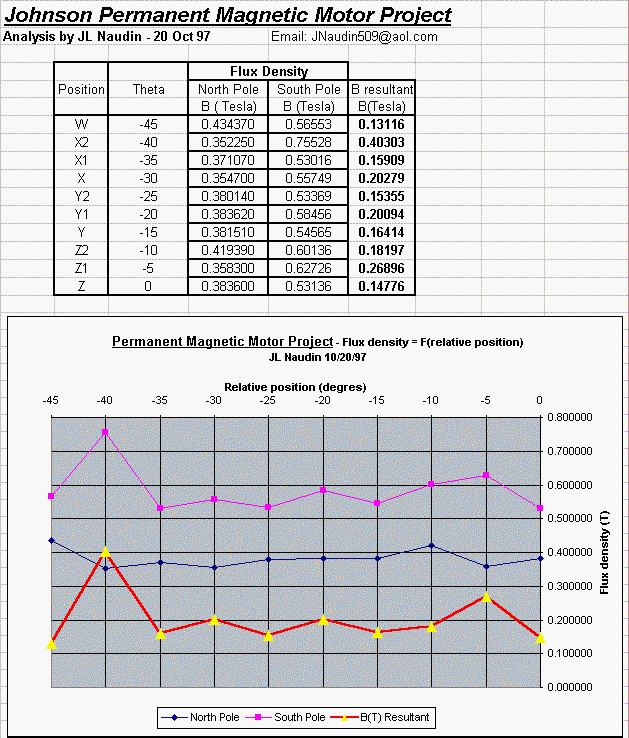
In the graphic below you see three
curves, this is the most decisive part.....
- the PINK
curve represents the flux density at the South pole of the magnet
actuator,
- the BLUE
curve represents the flux density at the North pole of the magnet
actuator,
- the RED
curve represents the resulting flux density between these two
poles, this is very important, and you notice that the resultant
flux density is ALWAYS POSITIVE, the continuous rotating
condition is now obtained with this setup, because the resulting
force is always oriented in the same direction, thus the PMM can
accelerate.....
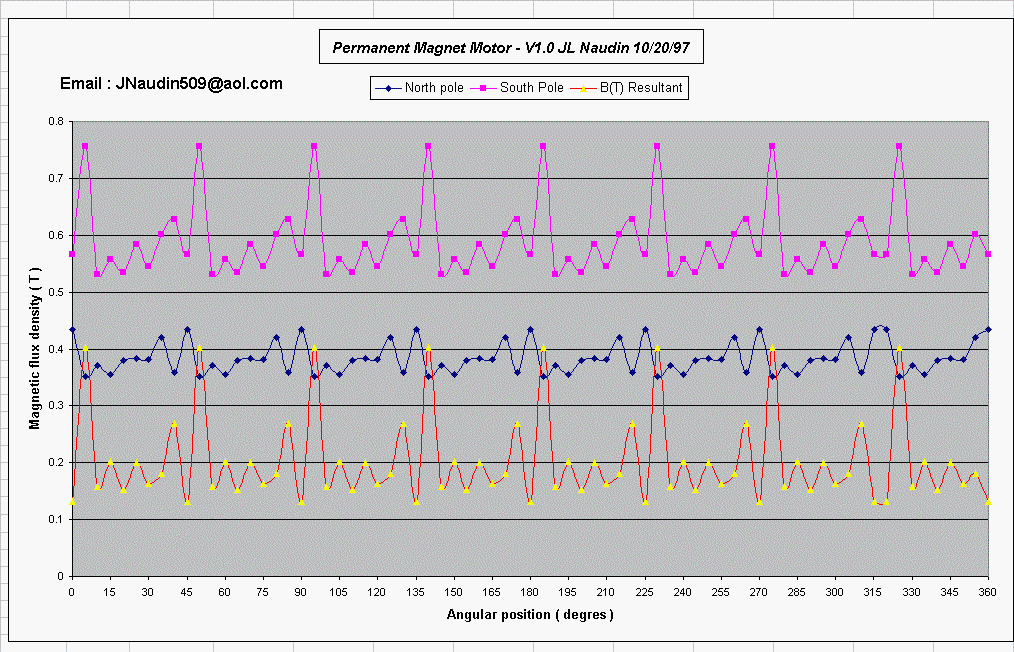
The last graphic shows the curves of the
magnetic flux density for a complete turn of 360 degres. As I
have said before the period is 45 degres and you can see for each
45 degres a "magnetic spike", this is the regauging
area.
We have an incremental periodic and asymetric potential (4 bumps),
the 4th bump is the regauging bump. This is the most difficult
part to tune, because in this area the flux density can be
reversed and this would stop the PMM.
If the Johnson is correctly built and finely tuned, we have the
possibility to violate the second law of the thermodynamics by
the use of the Rachet potentials. (see the document from
Dieter Bauer at: http://www.overunity.de/magmotor/magmotor.htm)
This motor has already been patented : US4151431 : Permanent magnet motor by H.R.Johnson
See also : The Johnson PM - Magnetic simulation
All comments and suggestions are welcome,
Jean-Louis Naudin
Return to the Quantum Electrodynamics page